Rumus Volume Tabung dan Contoh Soal yang Kerap Jadi Materi Pelajaran Sekolah

Ilustrasi Volume Tabung/Foto: iStock

Jakarta -

Bunda mungkin merasa pelajaran matematika Si Kecil di sekolah semakin sulit, ya? Si Kecil mungkin kini sudah mulai mempelajari berbagai jenis bangun ruang, termasuk tabung.

Bangun ruang merupakan sebutan untuk bangun tiga dimensi. Dalam pelajaran matematika, bangun ruang memiliki isi dan juga volume. Tak hanya itu, bangun ruang disebut memiliki bagian ruang yang dibatasi oleh himpunan titik-titik yang terdapat pada seluruh bangun tersebut.

Pada setiap bangun ruang tentunya memiliki rumusan dalam menghitung luas maupun isi atau volumenya.

Unsur-unsur bangun ruang

Pada bangun ruang terdapat beberapa unsur atau bagian-bagian yang membentuknya, Bunda. Berikut ini deretannya:

Titik sudut yang merupakan perpotongan tiga bidang sisi atau perpotongan tiga rusuk atau lebih.
Rusuk, yang merupakan pertemuan antara dua buah sisi atau perpotongan dua bidang sisi.
Sisi, yang merupakan sekat pembatas bagian dalam dan bagian luar suatu bangun.
Diagonal sisi atau bidang yang merupakan dua buah titik sudut yang berhadapan pada sebuah sisi atau garis, yang menghubungkan dua buah titik sudut yang tidak berurutan letaknya dan terletak pada sebuah sisi.
Diagonal ruang, yang merupakan dua buah titik sudut yang berhadapan pada sebuah bangun ruang atau garis yang menghubungkan dua buah titik sudut yang tidak beraturan letaknya dalam sebuah bangun ruang.

Jenis bangun ruang

Mengutip dari Buku Ajar Geometri karya Toybah dkk, bangun ruang terbagi menjadi dua macam, yakni bangun ruang sisi datar dan bangun ruang sisi lengkung.

Bangun ruang sisi datar

Bangun ruang sisi datar adalah bangun ruang yang memiliki sisi lurus. Contohnya seperti kubus, balok, prisma, dan limas. Berikut ini penjelasannya:

1. Kubus

Kubus adalah bangun ruang yang semua sisinya berbentuk persegi dan memiliki rusuk-rusuk yang sama panjang. Ciri-ciri kubus antara lain:

Memiliki enam bidang berbentuk persegi.
Mempunyai delapan titik sudut dan semua sudutnya siku-siku atau 90 derajat.
Mempunyai 12 rusuk yang sama panjang, 12 diagonal sisi, dan 4 diagonal ruang yang sama panjang.

2. Balok

Balok menurut Drs. Joko Untoro dalam buku Genius Matematika adalah bangun ruang yang dibatasi oleh enam bidang yang berbentuk persegi panjang dan sepasang-sepasang sama dan sebangun. Ciri-ciri balok antara lain:

Mempunyai 12 rusuk, enam sisi, dan delapan titik sudut.
Mempunyai delapan titik sudut dan semua sudutnya siku-siku atau 90 derajat.
Terbentuk dari empat sisi persegi panjang yang saling berhadapan sepasang-sepasang dan dua sisi persegi yang saling berhadapan.

3. Prisma

Prisma adalah bangun ruang yang dibatasi oleh dua buah bidang sejajar, kedua bidang sejajar ini merupakan bidang alas dan bidang tutup. Alas dan tutup prisma umumnya segitiga dan dikenal sebagai prisma tegak segitiga. Prisma tegak segitiga memiliki sembilan rusuk, lima sisi, dan enam titik sudut.

4. Limas

Limas adalah bangun ruang yang dibatasi oleh sebuah segi sebagai bidang alas dan beberapa bidang tegak berbentuk segitiga. Terdapat dua jenis limas, yaitu limas segitiga dan limas segiempat.

Bangun ruang sisi lengkung

Bangun ruang sisi lengkung adalah bangun ruang yang memiliki sisi lengkung seperti kerucut, bola, dan tabung. Berikut ini ulasannya:

1. Kerucut

Serupa, tapi tak sama, kerucut memiliki bentuk yang mirip seperti limas. Akan tetapi, alas dari kerucut adalah lingkaran, berbeda dengan limas yang beralaskan persegi. Kerucut memiliki dua sisi, yaitu alas dan selimutnya serta memiliki satu rusuk. Selain tabung, kerucut juga merupakan bangun ruang yang tidak memiliki titik sudut.

2. Bola

Bangun ruang sisi lengkung lainnya adalah bola. Si Kecil pasti sudah tidak asing dengan bola. Bangun ruang yang satu ini hanya memiliki satu sisi dan tidak mempunyai sudut. Volume bola dapat dihitung dengan rumus phi x r3.

3. Tabung

Cylinder podium with stairs and arch. Abstract background with various geometric shapes in pastel color for product presentation. Podium to show cosmetic products.

Ilustrasi Volume Tabung/ Foto: Getty Images/iStockphoto/Igishevamaria

Pernahkah Bunda melihat sebuah drum tempat minyak tanah atau oli? Drum ini merupakan salah satu bangun ruang yang berbentuk tabung. Tabung terdiri atas sisi alas dan sisi atas yang berbentuk lingkaran, serta sisi samping atau sisi lengkung di sepanjang tingginya.

Tabung atau silinder adalah bangun ruang tiga dimensi yang dibentuk oleh dua buah lingkaran yang identik dan sejajar. Tabung memiliki 3 sisi dan 2 rusuk.

Unsur-unsur tabung

Tabung/ Foto: Buku Belajar Matematika Aktif dan Menyenangkan

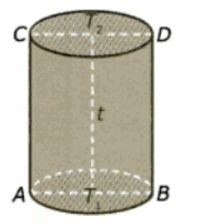
Amatilah gambar di atas, Bunda. Mengutip dari buku Belajar Matematika Aktif dan Menyenangkan karya Wahyudin Djumanta dan Dwi Susanti, terdapat beberapa bagian atau unsur tabung yang bisa diuraikan sebagai berikut:

Sisi yang diarsir (lingkaran T1) dinamakan sisi alas tabung. Sementara itu, sisi arsir lingkaran T2 dinamakan bagian atas tabung.
Titik T1 dan T2 masing-masing dinamakan pusat lingkaran (pusat sisi alas dan sisi atas tabung). Pusat lingkaran merupakan titik tertentu yang memiliki jarak yang sama terhadap semua titik pada lingkaran tersebut.
Titik A dan B pada lingkaran alas tabung, sedangkan titik C dan D pada lingkaran atas. Ruas T1A dan T1B dinamakan jari-jari lingkaran (jari-jari bidang alas tabung). Jari-jari lingkaran merupakan jarak pusat lingkaran ke titik pada lingkaran. Sementara itu jari-jari atas tabung adalah T2C dan T2D.
Ruas garis AB dinamakan diameter atau garis tengah lingkaran (diameter bidang alas). Diameter lingkaran merupakan ruas garis yang menghubungkan dua titik pada lingkaran yang melalui titik pusat lingkaran.
Ruas garis yang menghubungkan titik T1 dan T2 dinamakan tinggi tabung dan bisa dituliskan dengan 't'. Tinggi tabung disebut juga sebagai sumbu simetri putar tabung.
Sisi lengkung tabung yaitu sisi yang tidak diarsir, dinamakan selimut tabung. Adapun garis-garis pada sisi lengkung yang sejajar dengan sumbu tabung (ruas garis T1T2) dinamakan garis pelukis tabung.

Rumus luas permukaan tabung

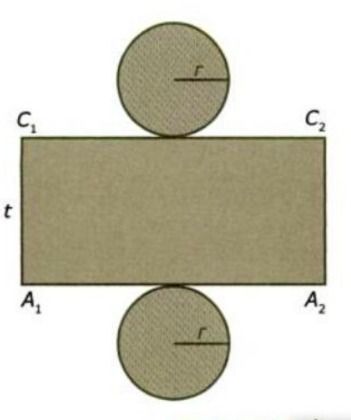
Jika gambar tabung sebelumnya direbahkan dan memotong garis ruas AC, keliling alas, dan keliling atasnya, sehingga menjadi bidang datar, maka akan terbentuklah gambar tabung seperti di bawah ini, Bunda.

Tabung/ Foto: Buku Belajar Matematika Aktif dan Menyenangkan

Selimut tabung berbentuk persegi panjang dengan ukuran sebagai berikut:

Panjang = keliling alas tabung = 2r
Lebar = tinggi tabung = t
Dengan begitu, luas selimut tabung = 2 phi.r x t

Luas permukaan tabung sama dengan luas jaring-jaringnya, yaitu:

L = luas selimut tabung + 2 x luas alas
L = 2 phi.r.t + (2 r.r)
L = 2 phi.r (t+r)

Sebagai catatan, phi tidak dapat dinyatakan secara tepat dalam bentuk desimal maupun pecahan, Bunda. Jadi, biasanya phi menggunakan bentuk desimal 3,14 atau pecahan 22/7.

Contoh soal luas permukaan tabung

1. Sebuah tabung berjari-jari 10 cm memiliki tinggi 30 cm dan phi = 3,14. Hitunglah luas permukaaannya.

Jawaban:

Diketahui r = 10 cm, t = 30 cm dan phi= 3,14.
L = 2.phi.r (t+r)
L = 2 x 3,14 x 10 (30 + 10) = 2.512.

2. Tinggi tabung adalah 10 cm dan jari-jari alas tabung adalah 7 cm. Tentukanlah luas selimut dan luas permukaan tabung.

Jawaban:

Luas selimut tabung
2.phi.t = 2 x 22/7 x 7 x 10 = 440 cm kuadrat.

Luas permukaan tabung

2.phi.r(t+r)
2 x 22/7 x 7 (10+7) = 748 cm kuadrat.

Volume tabung

Abstract realistic 3D white and green-blue steps cylinder pedestal podium set with pastel minimal wall scene for cosmetic product display presentation. Vector geometric rendering platform design.

Ilustrasi Volume Tabung/Foto: Getty Images/iStockphoto/Suppaluck Rainy

Ketika tabung terisi penuh, Bunda bisa menentukan ada berapa liter air, minyak, atau oli yang ada di dalam tabung tanpa mengeluarkan isinya. Bunda dapat menentukannya dengan cara menghitung daya tampung atau volume tabung.